Movimiento curvilíneo
Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es decir, el conjunto de puntos por los que pasa el móvil. Las magnitudes que describen un movimiento curvilíneo son:Vector posición r en un instante t.
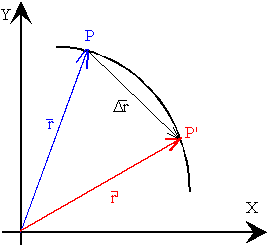 | Como la posición del móvil cambia con el tiempo. En el instante t, el móvil se encuentra en el punto P, o en otras palabras, su vector posición es r y en el instante t' se encuentra en el punto P', su posición viene dada por el vector r'.Diremos que el móvil se ha desplazadoDr=r’-r en el intervalo de tiempo Dt=t'-t. Dicho vector tiene la dirección de la secante que une los puntos P y P'. |
Vector velocidad
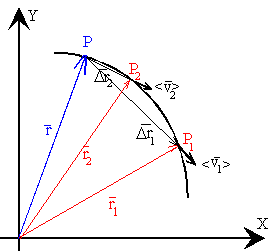 | El vector velocidad media, se define como el cociente entre el vector desplazamiento Dr y el tiempo que ha empleado en desplazarse Dt. El vector velocidad media tiene la misma dirección que el vector desplazamiento, la secante que une los puntos P y P1 cuando se calcula la velocidad media <v1> entre los instantes t y t1. |
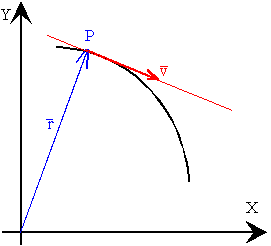 | El vector velocidad en un instante, es el límite del vector velocidad media cuando el intervalo de tiempo tiende a cero. Como podemos ver en la figura, a medida que hacemos tender el intervalo de tiempo a cero, la dirección del vector velocidad media, la recta secante que une sucesivamente los puntos P, con los puntos P1, P2....., tiende hacia la tangente a la trayectoria en el punto P. En el instante t, el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto. |
Vector aceleración
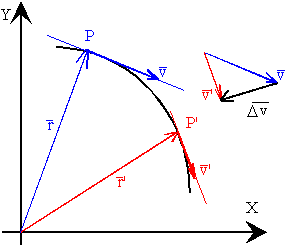 | En el instante t el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.En el instante t' el móvil se encuentra en el punto P' y tiene una velocidadv'. El móvil ha cambiado, en general, su velocidad tanto en módulo como en dirección, en la cantidad dada por el vector diferencia Dv=v’-v. |
No hay comentarios:
Publicar un comentario