Tercera ley de Newton o Ley de acción y reacción
Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.[6]
Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.
 , la fuerza de la partícula 1 sobre la partícula 2 es:
, la fuerza de la partícula 1 sobre la partícula 2 es:donde d la distancia entre las dos partículas y
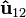 es el vector director unitario que va de la partícula 1 a la 2. Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:
es el vector director unitario que va de la partícula 1 a la 2. Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:Empleando la identidad vectorial
 , puede verse que la primera fuerza está en el plano formado por
, puede verse que la primera fuerza está en el plano formado por 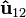 y
y  que la segunda fuerza está en el plano formado por
que la segunda fuerza está en el plano formado por 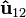 y
y  . Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, aunque son de igual magnitud.
. Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, aunque son de igual magnitud. 

No hay comentarios:
Publicar un comentario